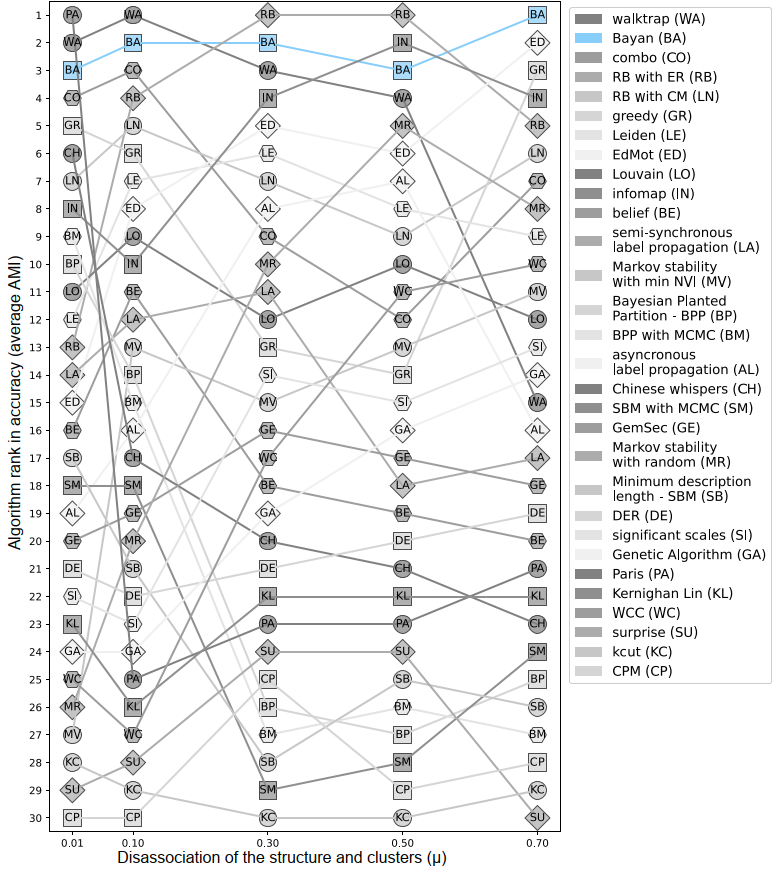
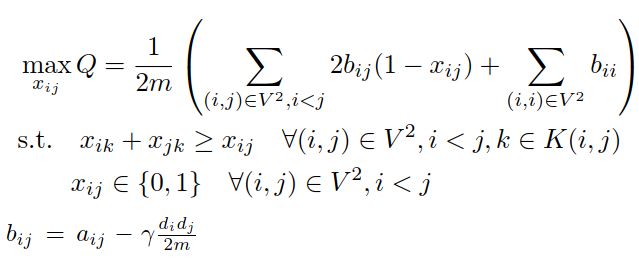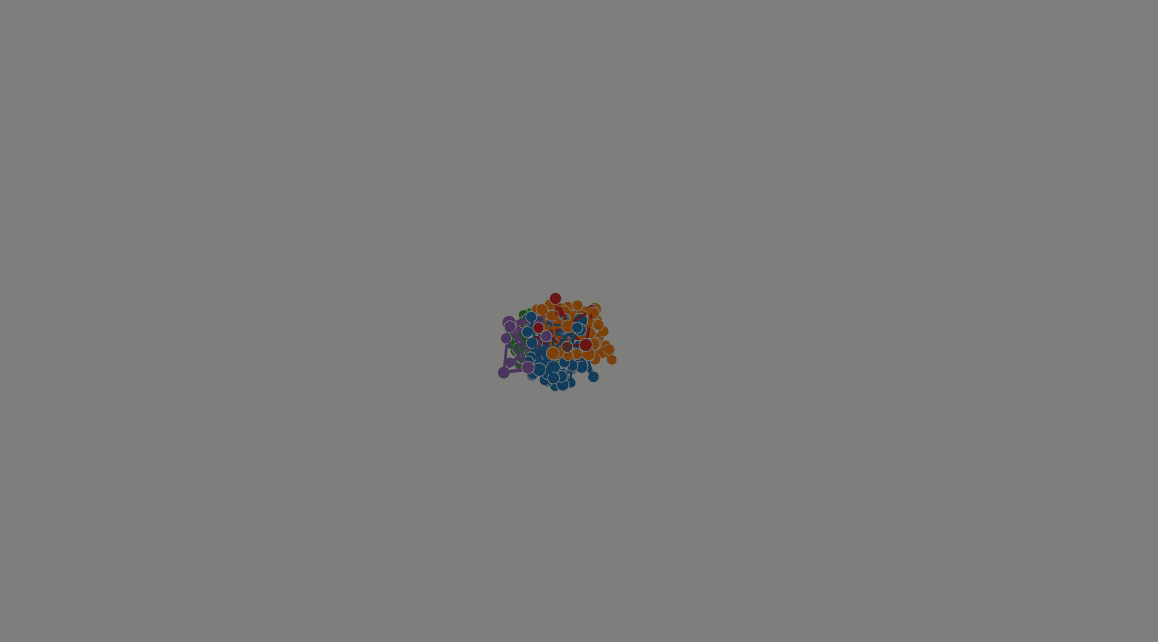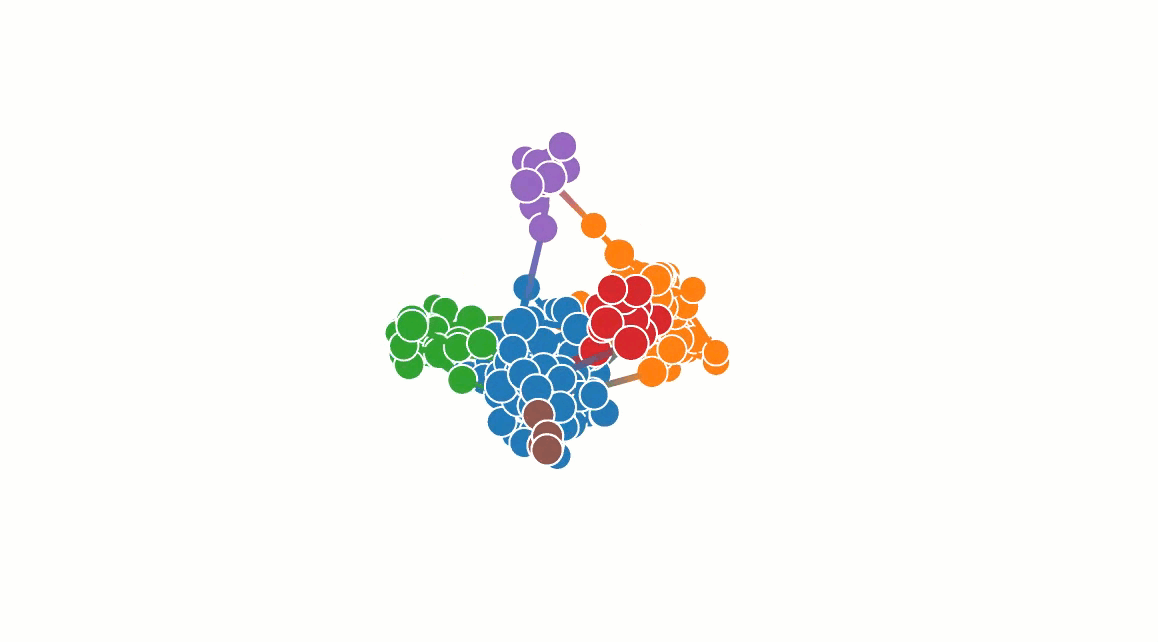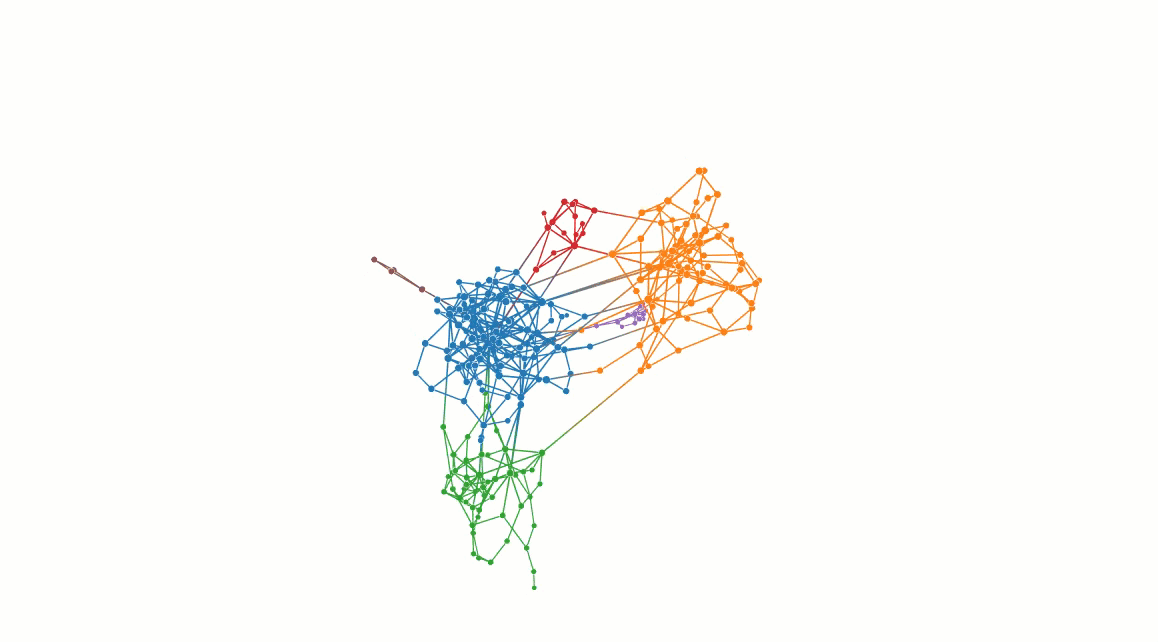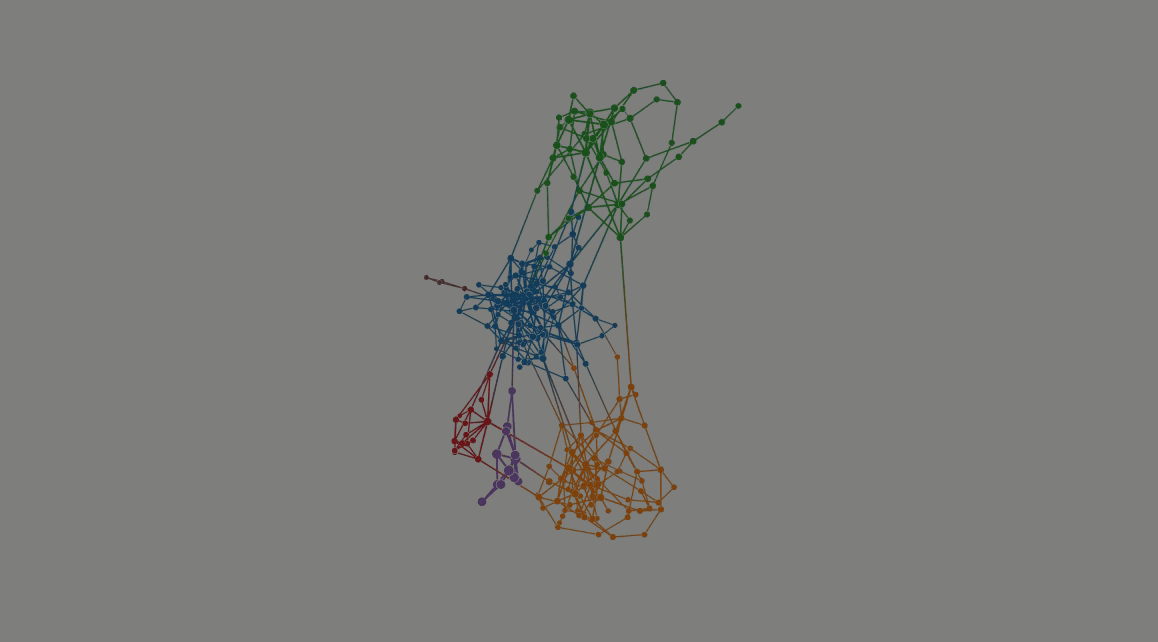What is Bayan project about?
Aim
- Developing a reliable and accurate algorithm for descriptive community detection in small and mid-sized networks, with optimality guarantees.
Community Detection
-
Descriptive community detection is the process of clustering the nodes of a network (graph) based on the structural patterns. It is an unsupervised task with a wide range of applications in life sciences (e.g., biological systems), social sciences (offline/online social networks), physical sciences (VLSI design, complex systems), mathematical sciences (agent-based models, computer vision), and even health sciences (drug discovery) (Wikipedia).
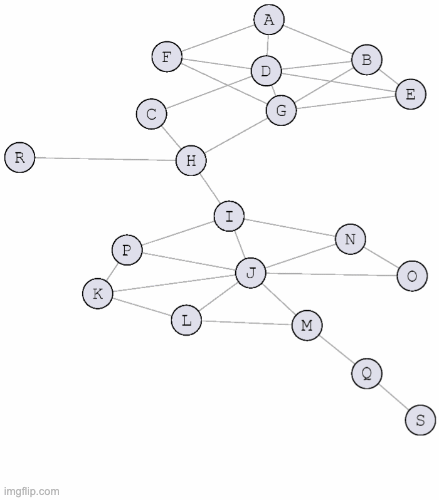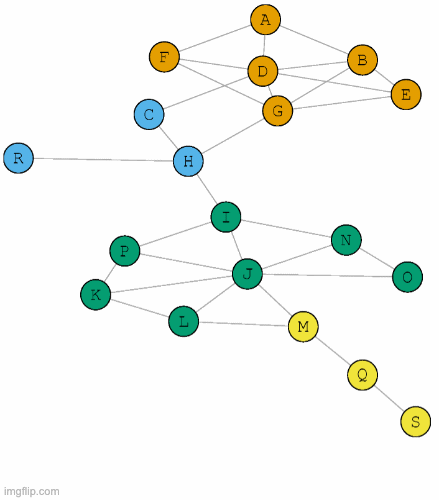
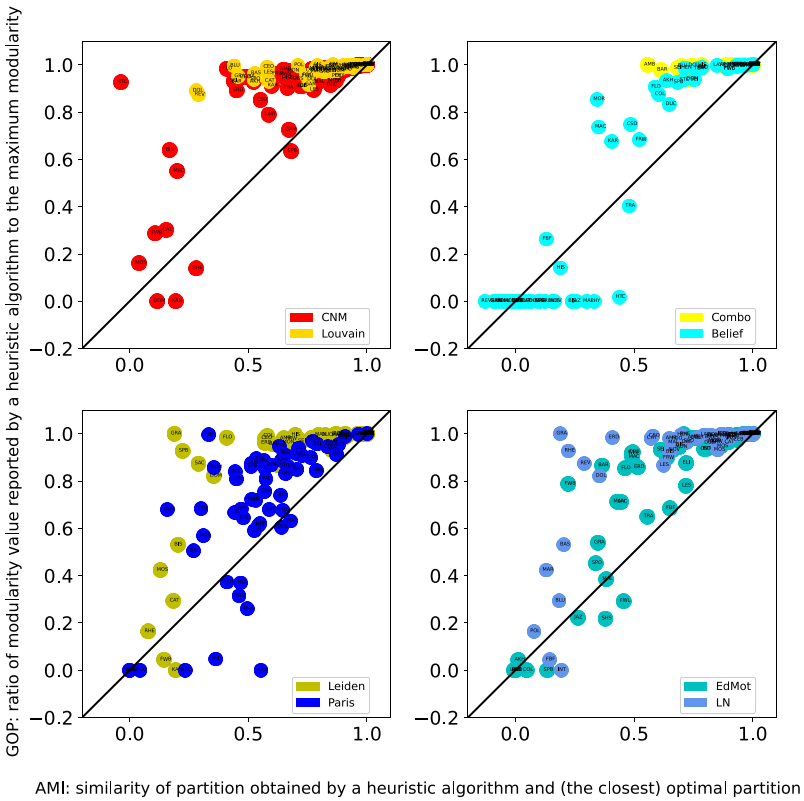
- There are several existing methods (algorithms) for approaching this computational problem. One family of algorithms attempts to find communities by maximizing modularity: a network-level quantity indicating the fraction of intra-community edges minus the expected fraction under a degree-preserving null model.